Christian Couderc

2 connectés # #

Processing et les cycles de la lune
courbes de Bezier

Introduction
Cycles lunaires
Première méthode, croissants par "curve"
Deuxième méthode, par courbes de Bezier
Conclusion

Maj : 04/02/22

Abstract :
Small page to discover the powerful and amazing functions of the brilliant engineer Bezier under Processing, allowing to realize all the complex curves in 2D or 3D. The pretext here is to modestly model the appearance of the phases of the moon.
Goes to Processing.org and check examples to discover this amazing world.

Résumé :
Petite page pour faire découvrir les puissantes et étonnantes fonctions du brillant ingénieur Bezier sous Processing, permettant de réaliser toutes les courbes complexes en 2D ou 3D.
Le prétexte est ici de modéliser modestement l’aspect des phases de la lune.
Allez sur Processing.org et consultez les exemples pour découvrir ce monde étonnant.

Introduction

Le but de cette page est de montrer les limites des outils curve et Bezier sous Processing en prenant comme exemple la représentation des croissants de la lune. Les divers exemples de mes pages servent à démystifier l'utilisation de Processing, outil formidable pour accéder aux animations graphiques.

Nous parlerons des courbes de Bezier, mais il faut auparavant se faire une idée, la page Wikipédia est très bien faite pour éclairer sur ce sujet, même si les développements mathématiques semblent complexes.
Leur utilisation est beaucoup plus simple, et les résultats sont étonnants quand on découvre leur puissance.
Cette page n’a d’intérêt que si vous voulez manipuler Processing et exécuter les programmes à charger.

Cycles lunaires

Pour rappel, la lune orbite sur une trajectoire elliptique à environ 384000 km, de la terre (1,3 seconde/lumière), c'est très proche.
Le cycle ou révolution synodique est d’environ 29 jours et demi, et les phases sont nommées et se déroulent ainsi :

Les limites de l'exercice

Attention, ceci n'est en rien un exposé d'astronomie et cela n’a aucune rigueur scientifique pour de multiples raisons :
Ici, la séparation ombre/lumière (cercle d'illumination) est brutale, dans la réalité les rayons du soleil rasants montrent le relief des cratères, et la ligne de séparation est pleine de détails qui sont absents sur ce modeste exercice.
La séparation n’apparait pas verticale, mais change d'injclinaison sous divers facteurs. Pour simplifier et ne pas alourdir par de longs calculs, cette variable sera oubliée.
L’opacité de l’ombre est variable, d’autant plus dense que l’ombre est étendue et la vitesse de déplacement n’est pas linéaire en fonction des jours, mais sinusoïdale, cela est simulé.

Le calcul du jour ne fait pas partie de ce propos, il existe sur le Net de nombreux exemples d’équations et de bibliothèques, nous nous contenterons d’utiliser un pointeur de jour entre 0 et 29,5 qui dessinera au mieux ce qui est représenté ci-dessus.

Nous calculons d'abord une variable en % marquant la position approximative de l'ombre (cercle d'illumination) ainsi :

0O% = nouvelle lune -> jour 0 ou 29.5
12.5% = premier croissant -> jour 3
25% = premier quartier -> jour 7
40% = gibeuse croissante jour 9
50% = pleine lune -> milieu du cycle, jour 14.75
60% = gibeuse décroissante jour 19
75% = dernier quartier -> jour 22
87.5% = dernier croissant -> jour 27

La feuille Excel de droite (jointe dans les logiciels) montre le calcul de la variation de la vitesse de déplacement, très ralentie en milieu du cycle et rapide pour les ombres étroites :

Le niveau de gris approximatif de l'ombre se calcule simplement :
int greyChannel = 5*(15-abs(int(day-moonCycle/2))) ;

Mais ceci est sans importance, venons en à la simulation de l'ombre. Dans cette page, les petites images ne sont pas cliquables pour s'agrandir, il faut lancer un des trois programmes sous Processing pour tester.

Les curseurs de jour sont au choix réglables à la souris ou en défilement automatique.

Première méthode, croissants par "curve"

C'est la première à laquelle on pense, car les arcs de cercle sont le moyen le plus simple pour dessiner des croissants.
Cela se fait en deux fois, le demi-cercle de droite, puis l'arc de cercle de gauche, sont rempli avec l'ombre.
Cela couvre tous les cas quand les formes à remplir sont concaves, mais pas entre les premier et dernier quartiers (jours 7 à 22),

Maintenant, autour de la pleine lune

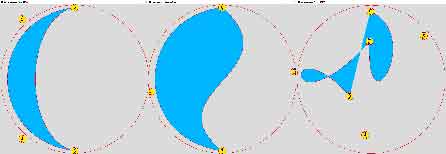
Problème insoluble, car il n'est pas possible de definir une forme avec deux arcs et la remplir. J'ai simulé en rouge une ombre de remplissage, la seule que l'on sait faire, ce n'est évidement pas ce que l'on cherche, mais du "remplissage en creux". On ne peut pas trouver de solution par la méthode "curve", essayez...

Curieusement, les vertex (voir la page Rolex sous Processing ) ne fonctionnent pas pour créer une forme avec des arcs de cercle.

Démonstration des courbes de Bezier

J'ai fait un petit bac à sable de démonstration qui est dans les fichiers joints, pour vous permettre de bien comprendre comment fonctionne une courbe de Bézier simplifiée, à tester sous Processing.

Il y a 4 points, les deux extrémités d'un segment et deux points d'influence. Vous pouvez déplacerchacun des points en cliquant dessus et en tirant doucement avec la souris et en voir les effets.
Cela n'a rien d'évident. Voici quelques exemples des formes que l'on obtient à partir d'un simple segment. Les courbes complexes sont constituées de suites de segments déformés.

Vous constatez que ces points d'influence "attirent et déforment" la courbe initiale d'autant plus qu'ils sont proches.

Deuxième méthode, croissants par courbes de Bezier

Pour dessiner les croissants, il y a deux cas, les remplissages concaves pour lesquels les arcs "curve" marchent aussi très bien, comme au dessus et les remplissages concaves qui sont maintenant possibles.
Nous utilisons ici les "Bezier Vertex". Les vertex ont été utilisés dans la page page Rolex sous Processing , cela consiste à définir un parcours de points reliant des segments et se refermant pour former une surface. Ici les segments seront déformés par des fonctions de Bezier.

Cette méthode permet de dessiner n'importe qu'elle forme très complexe en 2D ou 3D.

Examinez le source .pde pour voir les subtilités. L'animation vous montre que tout est maintenant possible.

Conclusion

Pour conclure, une de mes photos compressée de la lune, prise avec le Canon EOS 7D
Elle vous permet de constater que dans la vraie vie l'image que l'on voit du cercle d'illumination est diffuse et pleine de détails sur les cratères de la lune au niveau du cercle d’illumination que cette simulation en 2D ignore totalement.
Mais l'idée de cette page était de simplement faire découvrir à ceux qui ont eu le courage de lancer Processing, ce qu'il est possible de faire sur son écran avec un Arduino (et plus).

Mise à jour 21/06/2024

Vous trouverez tous les logiciels de cette page dans cette archive :
You will find all software of this page in this archive:

* Page vue 10509 fois IP : 18.221.102.0

Dernière retouche le 21 Juin 2024 à 11 h